Cubic equations of state are the standard in oil industry. They are successful because of their versatility, but users of cubic equations must accept minor deviations from experimental data for most physical properties. For some applications such deviations are unacceptable, one example being volumetric gas calculations. The commercial value of a given volume of gas is dependent on the weight of hydrocarbons as that determines the energy gained from burning the gas. Converting a given volume of gas to an equivalent weight amount requires an accurate Z-factor. Commercial PVT laboratories carry out Z-factor measurements by assuming a Z-factor of exactly 1.0 at atmospheric conditions, although published data shows that the Z-factor of a natural gas at atmospheric conditions is typically around 0.98 and could be as low as 0.95.
The GERG-2008 equation is the result of joined efforts among European gas companies (Group Europeén de Recherches Gazières) to develop a more accurate equation of state for natural gas mixtures (Kunz and Wagner, 2012). The GERG equation combines previously developed equations of state for pure gas components into an equation also applicable for multi-component gases. The underlying equations are expressed in terms of the Helmholtz free energy, A….
A = U – TS
U is internal energy, T absolute temperature, and S is entropy. It is practical to work in terms of Helmholtz energy because the properties needed in phase equilibrium and physical property calculations, like fugacities, enthalpies, and heat capacities are easily derived from the Helmholtz energy. GERG splits A into an ideal gas term and a residual term
A = Aig + Ares
For each mixture component Aig and Ares are found from expressions in density and temperature. As compared to a cubic equation, it adds a bit of complexity that GERG uses density and not pressure as specification variable as the pressure must be found in an iterative manner. Simple fundamental mixing rules allow Aig to be derived for a mixture. GERG has presented specific expressions for Ares of 7 binaries and generalized expressions for 8 other binaries. For the remaining binaries GERG uses combining rules averaging Ares of the individual components.
Figure 1 shows experimental Z factor data for a natural gas mixture together with simulation results for the GERG-2008 and the volume corrected SRK and PR equations. An almost perfect match is seen with the GERG-2008 equation and a comparison with a larger Z-factor data material shows that GERG-2008 will match experimental Z-factors of natural gases within ±0.1 %.
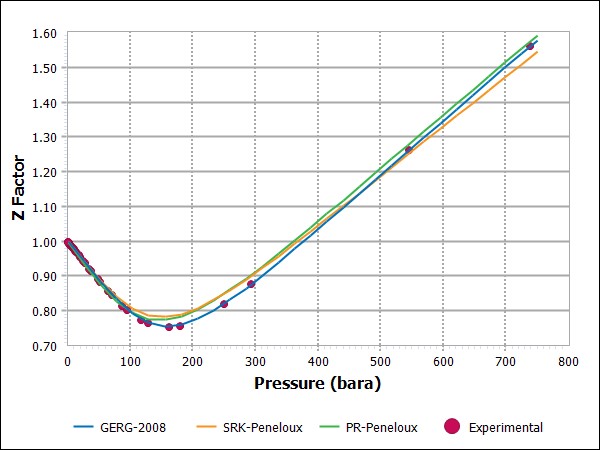
Figure 1 Experimental and simulated results for Z-factor of a natural gas at 17.85oC (Mollerup and Angelo, 1985)
Figure 2 shows experimental and simulated data for the Joule-Thomson coefficient of another natural gas. Again the GERG-2008 equation stands out and gives a very good match of the data.

Figure 2 Experimental and simulated results for Joule-Thomson coefficient of a natural gas at 600 psia (Sage et al., 1943)
Calsep introduced GERG-2008 in PVTsim Nova version 2 released in 2015. The GERG equation is currently limited to mixtures of 20 defined components with nC10 as the heaviest component. We have received requests about a possible future extension of GERG to also handle mixtures with undefined C7+ fractions. GERG-2008 is based on an extensive data material for each component in pure form. For components heavier than C10 there is not as extensive a data material to draw on as for lighter components. An extension with C11-C15 components could be an option, but it is unlikely that GERG will ever be an equation applicable also for oil systems. GERG-2008 is most likely to remain as a useful tool for simulations on natural gas mixtures when a high accuracy is required.
REFERENCES
Kunz, O. and Wagner, W., “The GERG-2008. Wide range equation of state for natural gases and other mixtures. An expansion of GERG-2004.” J. Chem. Data 57, 2012, pp. 2031-3091.
Mollerup, J. and Angelo, P., Measurement and correlation of the volumetric properties of a synthetic natural gas mixture, Fluid Phase Equilibria 19, 1985, pp. 259-271.
Sage, B.H., Botkin, D.F. and Lacey, W.N., Joule Thompson coefficients for two natural gases, SPE-943216-G, Trans AIME 151, 1943, pp. 216-220.